
EL DETERMINANTE
El determinante es una función que le asigna a una matriz de orden n, un único número real llamado el determinante de la matriz. Si A es una matriz de orden n, el determinante de la matriz A lo denotaremos por det(A) o también por (las barras no significan valor absoluto).

INVERSA POR ELIMINACION GAUSSIANA
Es posible usar la eliminación gaussiana para encontrar inversa de matrices n × n. Para ello se aumenta la matriz dada, digamos A con una matriz identidad, simplemente escribiendo las filas de la identidad a continuación de las de nuestra matriz A, por ejemplo dada:

El proceso ha finalizado porque en la parte izquierda tenemos la forma escalonada reducida de A y puesto que ésta
El proceso ha finalizado porque en la parte izquierda tenemos la forma escalonada reducida de A y puesto que ésta es la matriz identidad entonces A tiene inversa y su inversa es la matriz que aparece a la derecha, en el lugar que al principio ocupaba la identidad. Cuando la forma escalonada reducida que aparece no es la identidad es que la matriz de partida no tiene inversa.
NOTA : EL VIDEO PLANTA LA INVESA DE MATRIZ POR TRANSPUESTA.
REFUERZA UN POCO MAS ??''
VIDEO 1 : https://www.youtube.com/watch?v=3BpGef99HEs


 L
L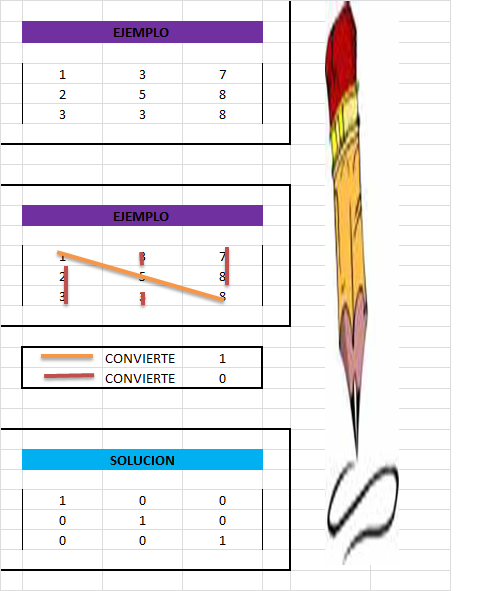


 U
U






